Chapitre I - L`approche de Langevin pour le mouvement

Nota : il s’agit d’une premi`ere version des notes de cours. Merci de signaler les erreurs `a
[e-mail] version du 16 septembre 2015
Chapitre I - L’approche de Langevin pour le mouvement Brownien
But du chapitre : discuter du sens physique de l’´equation de Langevin (fluctuations, r´eponse `a
une force ext´erieure . . . ). Mettre au jour le lien entre fluctuations et dissipation.
Un vice de forme s’est gliss´e dans la discussion. . . lequel ? (r´eponse `a la fin du chapitre).
1 Collo¨ıdes et mouvement Brownien
En 1827, le botaniste R. Brown d´ecouvre que de petits grains de pollen (∼1µm), immerg´es
dans un fluide, ont un mouvement erratique, compliqu´e et incessant. Il remarque que le mˆeme
ph´enom`ene se produit avec des petits min´eraux. C’est une observation importante car elle exclut
une quelconque force vitale qui serait propre aux objets biologiques. De mani`ere g´en´erale, tout
objet de taille m´esoscopique (interm´ediaire entre micro et macro) exhibe le mˆeme mouvement dit
Brownien : [1] les objets ne doivent pas ˆetre trop gros, pour ˆetre sensibles `a l’agitation thermique,
[2] tout en ´etant beaucoup plus massifs que les mol´ecules du fluide porteur.
•La contrainte [1] impose, pour un collo¨ıde sph´erique de rayon σet de densit´e de masse ρ:
(ρ g σ3)σ < kT (o`u ggravit´e)
⇒σ < kT
ρg 1/4
∼ 1
40 eV
103.10!1/4
∼10−20
1041/4
∼10−6m
•La contrainte [2] impose grosso modo :
σ > 10−8ou 10−9m
֒→taille comprise entre 10−8et 10−6m (dans un solvant comme l’eau)
On parle de collo¨ıdes, d´efinis initialement par le chimiste ´ecossais T. Graham dans les
ann´ees 1860 comme ´etant des substances qui ne diffusent pas `a travers des membranes semi-
perm´eables, ce qui conduit `a la mˆeme contrainte de taille que ci-dessus : σ > 10−9m ; ces
substances se pr´esentaient souvent sous formes de gommes, de colles (κσλλα en grec, d’o`u le
nom “collo¨ıdes”). Synonyme aujourd’hui : mati`ere molle, ce qui ne fait pas trop mal quand
on le re¸coit dans la figure.
L’id´ee que le mouvement d’un collo¨ıde ´etait dˆu aux collisions incessantes avec le fluide por-
teur s’est r´epandue `a la fin du XIXi`eme si`ecle, et c’est Einstein qui a le premier propos´e une
explication claire du ph´enom`ene (1905). Les exp´eriences sur l’´equilibre de s´edimentation par
Jean Perrin (prix Nobel 1926) en ont donn´e une confirmation exp´erimentale, ainsi qu’une
mesure du nombre d’Avogadro (fondement de la th´eorie atomique de la mati`ere). On doit
mentionner toutefois que les lois fondamentales du mouvement Brownien avaient ´et´e obtenues
un peu auparavant par Louis Bachelier dans sa th`ese “Th´eorie de la sp´eculation” (1900),
mˆeme si les objets consid´er´es ´etaient bien diff´erents. Enfin, historiquement, c’est dans le cadre
de l’´etude du mouvement Brownien que le premier processus stochastique a ´et´e construit (N.
Wiener 1923). Point important pour l’histoire des math´ematiques. Ce domaine a ´et´e mis `a
l’honneur avec la m´edaille Fields de Wendelin Werner en 2006, de nouveau en 2010 avec
Stanislas Smirnov puis en 2014 avec Martin Hairer, qui se sont vus d´ecerner la mˆeme
r´ecompense.
1

֒→les id´ees et m´ethodes qui vont suivre d´epassent largement le cadre des suspensions
collo¨ıdales. Elles sont applicables `a la classe de ph´enom`enes o`u le bruit joue un rˆole impor-
tant (biologie, finance, chimie...).
2 Le mod`ele de Langevin
Par souci de simplicit´e : traiter le probl`eme `a une dimension ; g´en´eralisation `a dimension d
imm´ediate. Dans les premi`eres approches (Einstein,Schmoluchowski), l’inertie des collo¨ıdes
´etait n´eglig´ee. Langevin a propos´e un raisonnement plus ´elabor´e [CRAS 146, 530 (1908)]. On
s’int´eresse au centre de masse du collo¨ıde x(t) :
v=dx
dt et mdv dt =Fext +FUN SEUL COLLOIDE ICI
La force Fest due aux interactions avec le fluide porteur, suppos´e `a l’´equilibre `a la temp´erature T.
Fonction d´esesp´er´ement compliqu´ee (fluide porteur constitu´e d’un grand nombre de mol´ecules)
mais poss`ede deux caract´eristiques essentielles :
(a) fluctue sur une ´echelle de temps τc∼temps de collision (faible, disons ∼10−15 s pour fixer
les id´ees, voire moins), en raison de la succession des impacts mol´eculaires
(b) si la particule est soumise `a une force ext´erieure Fext que l’on arrˆete brusquement, la vitesse
moyenne 1de la particule doit ˆetre amortie par les collisions avec les mol´ecules du fluide,
ce qui donne une friction d’autant plus grande que vest grande (penser par exemple `a la
friction de Stokes 2)
FStokes =−6π η σ v pour une sph`ere de rayon σ, o`u η: viscosit´e dynamique
=−4π η σ v avec des conditions aux limites “slip” (par opposition `a “stick”)
La force Fne d´epend pas explicitement du temps, mais implicitement, via les coordonn´ees de
la particule et de toutes celles des mol´ecules du fluide porteur. Il faudrait r´esoudre toutes les
´equations du mouvement coupl´ees... Fort des remarques a) et b) ci dessus, le mod`ele de Lange-
vin court-circuite ces probl`emes en d´ecrivant le mouvement par une ´equation ph´enom´enologique.
mdv
dt =−m γ v(t) + R(t) + Fext ´equation de Langevin (1)
o`u le coefficient de friction γest constant [γ] = 1
tps et R(t) est une force al´eatoire ind´ependante
de v, appel´ee force de Langevin. L’impossibilit´e de caract´eriser enti`erement l’´etat du syst`eme
global impose le recours `a une description statistique, bas´ee sur une moyenne d’ensemble.
On consid`ere une collection d’un grand nombre Nde syst`emes, avec mˆemes valeurs de xet
v, mais diff´erant par les degr´es de libert´e du fluide (on parlera de r´ealisations du bruit) :
hR(t)i=1
N
N
X
i=1
R(i)(t) =⇒h i commute avec d
dt ,d dx ,Zdt
En d’autres termes, il s’agit d’une moyenne d’ensemble, sur la fonction de distribution du fluide
porteur (`a l’´equilibre, et donc de poids de Boltzmann bien d´efini). On peut aussi consid´erer que
1. prendre par exemple la moyenne sur un grand nombre de collisions, mais sur une ´echelle de temps suffisam-
ment petite pour que vn’ait pas ´evolu´e. . . , cf discussions `a venir
2. On suppose implicitement les nombres de Reynolds petits. Re =U.L/ν o`u νest la viscosit´e cin´ematique
ν=η/ρ = 10−3/103= 10−6m2/s pour l’eau. Donc, pour L= 1 µm, tant que U≪1 m/s, on a Re ≪1.
2

la moyenne porte sur un grand nombre de particules dans le mˆeme fluide, `a condition que les
collo¨ıdes n’interagissent pas (grande distance mutuelle = r´egime dilu´e).
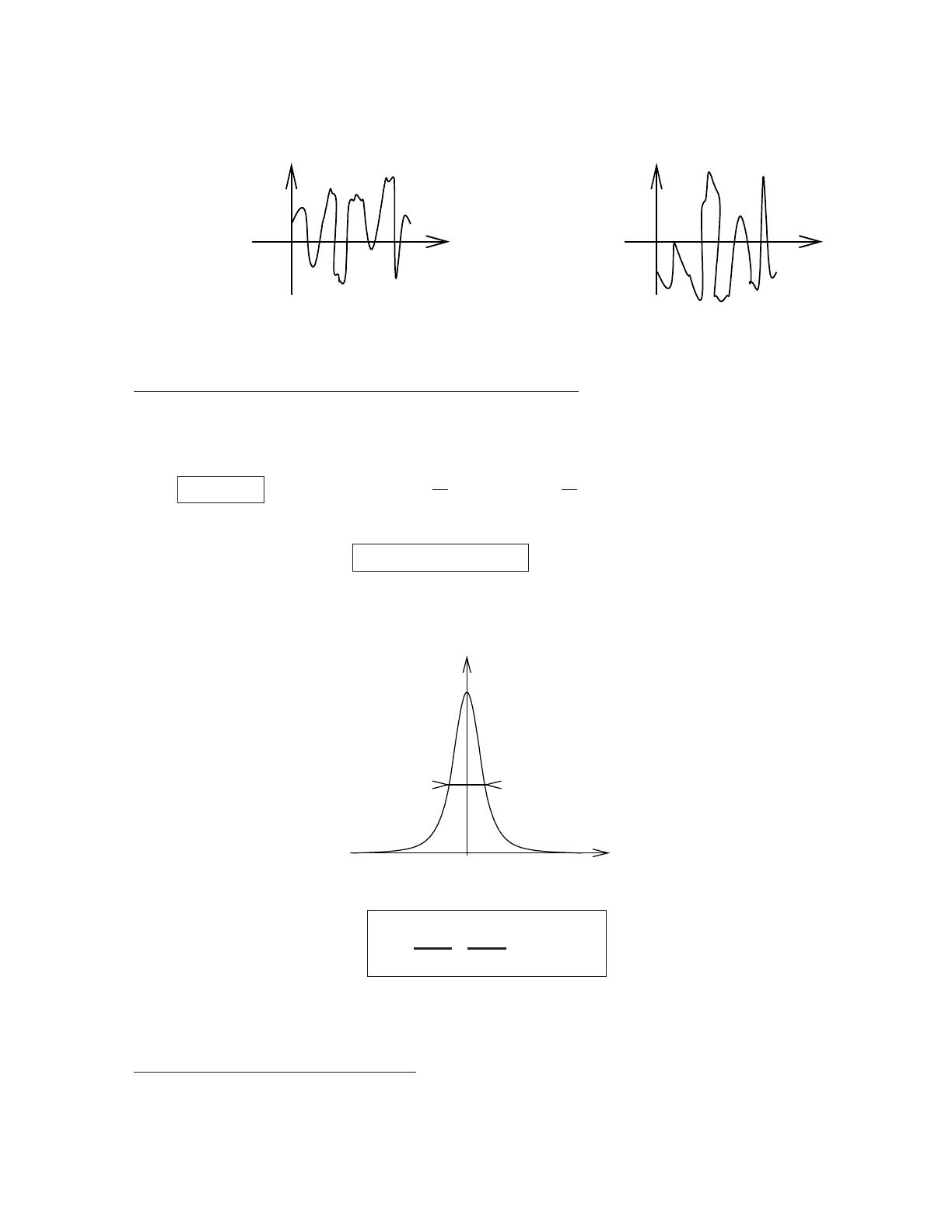
(1) (2)
R
↔
τc
Syst`eme 1 Syst`eme 2
t t
R
Hypoth`eses sur la force de Langevin R(t), et cons´equences
* Fluide dans un ´etat stationnaire, `a l’´equilibre : moyennes `a un temps ne d´ependent pas du
temps, et hR(t)R(t′)ine d´epend que de t−t′
*hR(t)i= 0 . Pour Fext = 0, on a d
dthvi=−γhvi+1 mhRi. Si l’on veut avoir hvi= 0 aux
temps longs, on doit avoir hRi= 0.
* Fonction de corr´elation C(τ) = hR(t)R(t+τ)iest suppos´ee connue. Elle d´ecroˆıt tr`es vite
avec τ, sur ´echelle τc(temps de collision ∼temps de corr´elation de R). Fonction d’auto
corr´elation stationnaire ⇒fonction paire 3de τ. Elle v´erifie 4| C(τ)|6C(0).
τ
C(τ)
τc
On pose : Z∞
0hR(t)R(t+τ)i
|{z }
C(τ)
dτ = Γ m2(2)
On ne doit pas oublier que friction −γm v et force al´eatoire Rsont deux facettes d’un mˆeme
ph´enom`ene : collisions avec le fluide ⇒γet Γ sont reli´es, via une formule qui d´ecoule de la
condition d’auto-coh´erence de l’approche (cf plus loin).
3. Dans le cas complexe, on consid´ererait C(τ) = hR(t)R∗(t+τ)i. La stationnarit´e se traduit alors par
C(τ) = hR(t−τ)R∗(t)i=C∗(−τ)
4. On peut noter que hA(t)B(t+τ)id´efinit un produit scalaire, d’o`u | C(τ)|6C(0) (Cauchy-Schwartz).
Par ailleurs, rien n’interdit `a la fonction de corr´elation Cde devenir n´egative.
3

Si τcest beaucoup plus court que tous les autres temps du probl`eme, une bonne approximation est
C(τ)∝δ(τ) d’o`u C(τ) = 2 Γ m2δ(τ) . L’ordre de grandeur de C(0) est Γm2/τc. Il est important
de ne jamais perdre de vue que τcn’est jamais strictement nul.
3 Diffusion, relaxation et r´eponse
3.1 ´ Evolution de la vitesse
Dans ce qui suit, on suppose Fext = 0, sauf mention du contraire, et C(τ) = 2Γ m2δ(τ). A
t= 0, on a v=v0. L’´equation m˚v=−γ m v +R(t) s’int`egre par “variation de la constante”
v(t) = A(t)e−γt ⇒m˚ A e−γt =R(t)
⇒v(t) = v0e−γt +1
mZt
0
R(t′)e−γ(t−t′)dt′(3)
−→ moyenne de v(t) : hv(t)i=v0e−γt →amortissement avec temps caract´eristique γ−1
−→ variance de v(t) : σ2
v≡ h(v− hvi)2i=hv2i − hvi2, carr´e de l’´ecart type.
⇒σ2
v=1
m2Zt
0
dt′Zt
0
dt′′ hR(t′)R(t′′)i
|{z }
2m2Γδ(t′−t′′ )
e−γ(t−t′)e−γ(t−t′′ )
= 2Γ Zt
0
e−2γ(t−t′)dt′=Γ
γ1−e−2γt
(4)
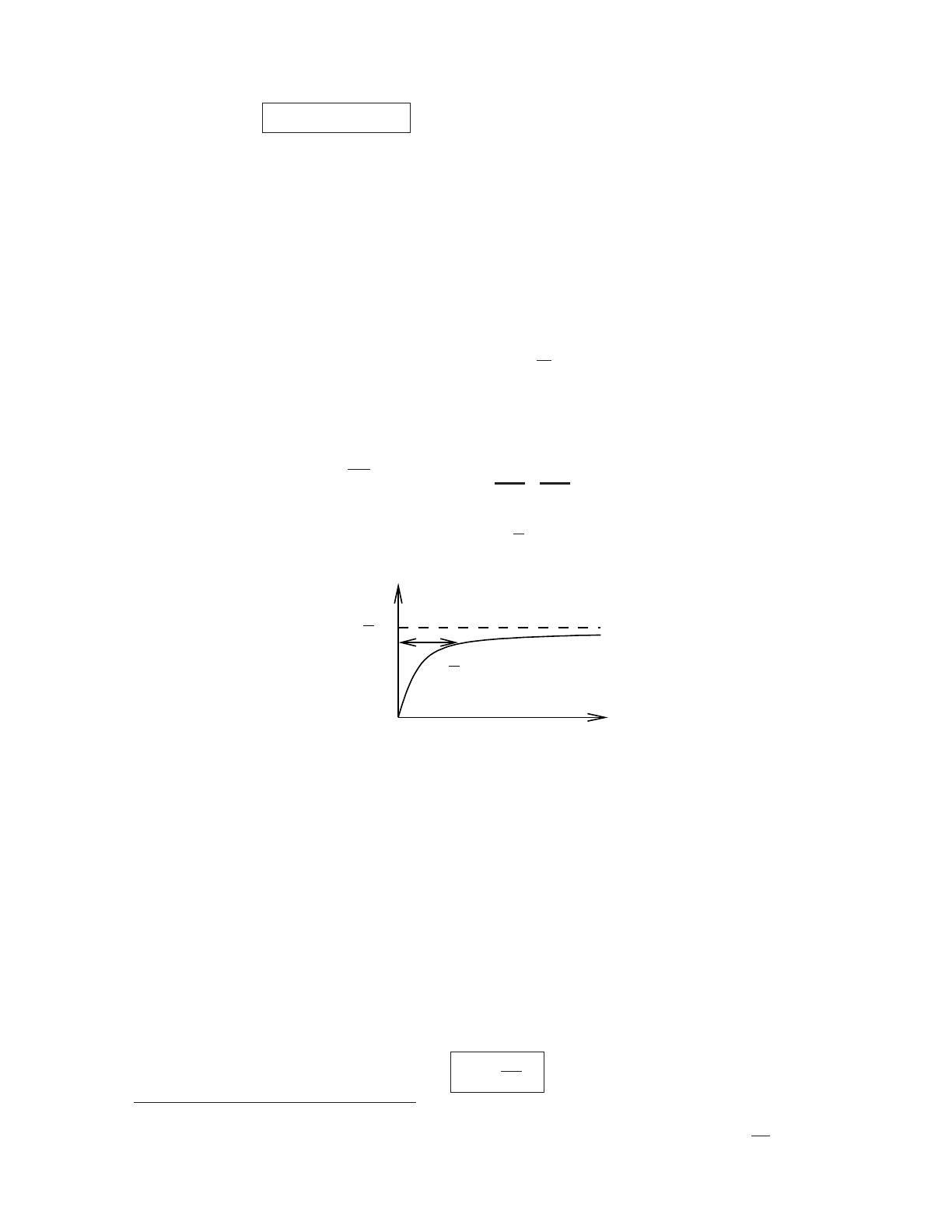
σ2
v
Γ
γ
1
γ
t
0
•t= 0 : σ2
v= 0 (vitesse certaine). Puis, sous l’effet de la force al´eatoire, les fluctuations
apparaissent.
•t≪γ−1:σ2
v∼2 Γ t. Diffusion dans l’espace des vitesses, Γ est le coefficient de diffusion. A ces
´echelles de temps la friction est inop´erante, et on a m˚v=R→version continue d’une marche
al´eatoire (faire l’identification v→x, position du marcheur). Les “coups” re¸cus par la variable
vproduisent une diffusion standard.
•t≫γ−1: la friction agit et σ2
vsature `a Γ/γ. Equation compl`ete →marcheur al´eatoire retenu
par les bretelles 5(force harmonique ˚x=−γx +R). Le marcheur ne diffuse qu’aux temps courts
(o`u il ne sent pas ses bretelles).
3.2 Une premi`ere relation de fluctuation-dissipation
Aux temps longs, la particule doit se thermaliser avec un bain `a temp´erature T, d’o`u hv2i=
kT/m. Puisque hvi → 0 pour t≫γ−1, on a 6σ2
v∼Γ/γ ∼kT/m
⇒γ=m
kT Γ(5)
5. Bretelles : braces (GB), suspenders (US)
6. Ecrire Γ = γ kT /m qui se comprend comme le coefficient de diffusion dans l’espace des v→[v]2
tps =γ kT/m
4

Peut se r´e´ecrire
γ=1
2mkT Z∞
−∞hR(t)R(t+τ)idτ γ≡dissipation ; hR(t)R(t+τ)i ≡ fluctuation
Relation ´egalement valable pour τcnon nul, pourvu que τc≪γ−1. Elle porte parfois le nom
de seconde relation de fluctuation-dissipation (il en existe en effet une autre, qui relie γaux
fluctuations de vitesse, et qui apparaˆıtra sous peu). Cela traduit le fait que les collisions sont
`a l’origine de la friction et de la force fluctuante. Pour l’´equation de Langevin retard´ee (ou
g´en´eralis´ee), nous retrouverons une formulation tr`es proche [Eq. (48)].
3.3 ´ Evolution de la position
At= 0, on suppose x=x0= 0 et v=v0. On int`egre (3)
x(t) = v0
γ(1 −e−γt) + 1 mZt
0
dt′Zt′
0
dt′′ R(t′′)e−γ(t′−t′′ )⇒ hx(t)i=v0
γ(1 −e−γt) (6)
qui varie de 0 `a v0/γ. Pour obtenir la variance de la position, on peut calculer σ2
x=h(x−hxi)2i=
hx2i − hxi2via
d
dt σ2
x= 2 h(x− hxi)(v− hvii
=2
m2Zt
0
dt′Zt′
0
dt′′ Zt
0
dt′′′hR(t′′)e−γ(t′−t′′ )R(t′′′)ie−γ(t−t′′′ )
= 4Γ Zt
0
dt′Zt′
0
dt′′ exp −γ(t′−t′′)−γ(t−t′′)
=2 Γ
γ2(1 −e−γt)2
(7)
et comme σ2
x(t= 0) = 0 (xest une variable certaine `a t= 0) ; il vient
σ2
x=2Γ
γ2t+1 2γ(1 −e−2γt)−2 γ(1 −e−γt)(8)
•t≪γ−1:σ2
x∝t3,et hxi ∝ t⇒ hx2i ∼ hxi2∼v2
0t2. R´egime balistique aux temps courts,
tant que la friction n’a pas pu agir.
•t≫γ−1σ2
x∼2Γ/γ2t∼ hx2iet hxi → constante. R´egime diffusif avec coefficient de
diffusion D= Γ /γ2=kT/(mγ) . Pour un rappel sur la diffusion en dimension d, voir page 6.
Mentionnons ici que l’on peut obtenir une relation plus simple que (6) pour la position, en
int´egrant le e−γt′par partie 7
x(t) = x0+v0
γ(1 −e−γt) + 1 mγ Zt
0h1−e−γ(t−t′)iR(t′)dt′.(9)
Cela permet de trouver rapidement le r´esultat (8).
7. En effet, en notant F′la d´eriv´ee d’une fonction F:
Zt
0
dt′e−γt′Zt′
0
dt′′ R(t′′ )eγt′′
|{z }
F(t′)
="−e−γt′
γF(t′)#t
0
+Zt
0
e−γt′
γF′(t′)
|{z}
R(t′) exp(γt′)
dt′
=−eγt
γZt
0
dt′R(t′)eγt′ +1
γZt
0
R(t′)dt′
=1
γZt
0h1−e−γ(t−t′)iR(t′)dt′
5